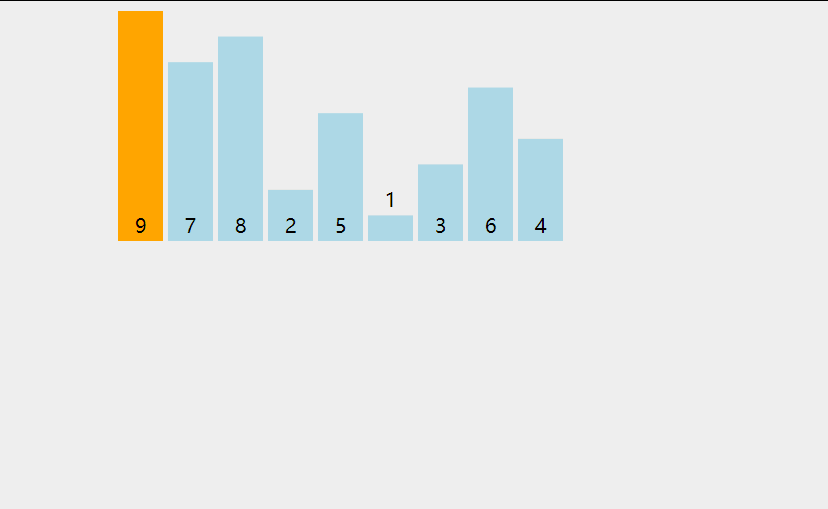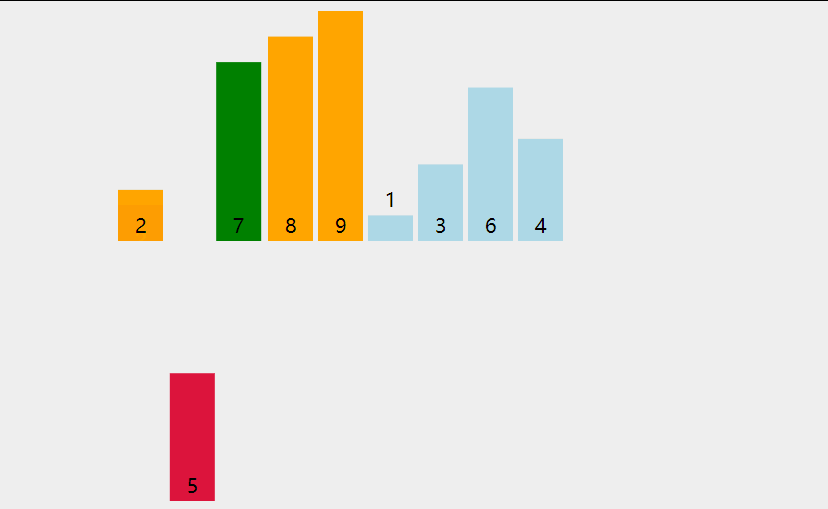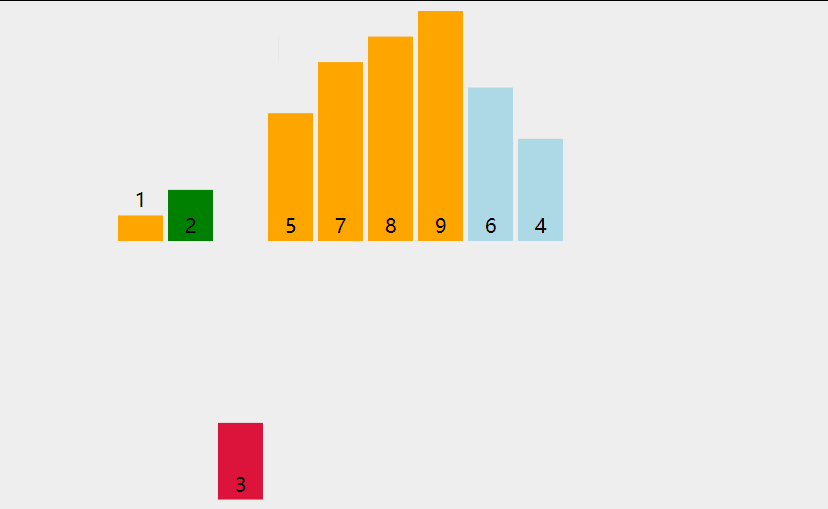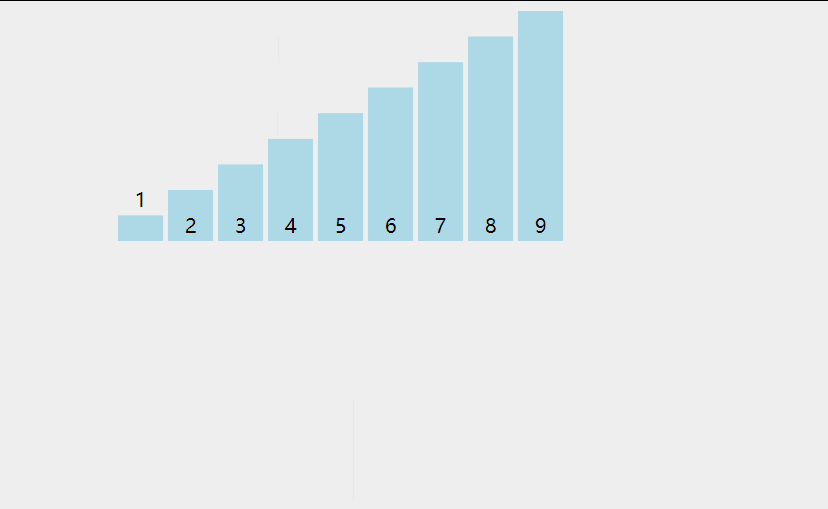搜索到
1
篇与
的结果
-
 排序算法 - 5.插入排序 插入排序的原理: 一般也被称为直接插入排序。对于少量元素的排序,它是一个有效的算法 。插入排序是一种最简单的排序方法,它的基本思想是将一个记录插入到已经排好序的有序表中,从而得到一个新的、记录数增 1 的有序表。在其实现过程使用双层循环,外层循环对除了第一个元素之外的所有元素,内层循环对当前元素前面有序表进行待插入位置查找,并进行移动 。 选择排序的基本思想是: 将未排序的元素一个一个地插入到有序的集合中,插入时把所有有序集合从后向前扫一遍,找到合适的位置插入。 public static void main(String[] args) { int[] arr = {1456, 22, 2378, 7867, 14, 87, 57, 9, 3}; //默认认为第一个元素是排序好的,所以从第二个元素开始 for (int i = 1; i < arr.length; i++) { //从当前 i 的这个元素的前一个位置开始,往最前面找 for (int j = i; j > 0; j--) { //如果找到比一个小的数,就交换一下 if (arr[j]<arr[j - 1]) { swap(arr, j, j - 1); } //发现前面的数比 i 大, 说明前面已经没有比它更小的了 无需再找,退出本次循环 else { break; } } } for (int i : arr) { System.out.println(i); } } private static void swap(int[] arr, int indexA, int indexB) { int temp = arr[indexA]; arr[indexA] = arr[indexB]; arr[indexB] = temp; } 平均时间复杂度:O(N^2) 最差时间复杂度:O(N^2) 空间复杂度:O(1) 排序方式:In-place 稳定性:稳定
排序算法 - 5.插入排序 插入排序的原理: 一般也被称为直接插入排序。对于少量元素的排序,它是一个有效的算法 。插入排序是一种最简单的排序方法,它的基本思想是将一个记录插入到已经排好序的有序表中,从而得到一个新的、记录数增 1 的有序表。在其实现过程使用双层循环,外层循环对除了第一个元素之外的所有元素,内层循环对当前元素前面有序表进行待插入位置查找,并进行移动 。 选择排序的基本思想是: 将未排序的元素一个一个地插入到有序的集合中,插入时把所有有序集合从后向前扫一遍,找到合适的位置插入。 public static void main(String[] args) { int[] arr = {1456, 22, 2378, 7867, 14, 87, 57, 9, 3}; //默认认为第一个元素是排序好的,所以从第二个元素开始 for (int i = 1; i < arr.length; i++) { //从当前 i 的这个元素的前一个位置开始,往最前面找 for (int j = i; j > 0; j--) { //如果找到比一个小的数,就交换一下 if (arr[j]<arr[j - 1]) { swap(arr, j, j - 1); } //发现前面的数比 i 大, 说明前面已经没有比它更小的了 无需再找,退出本次循环 else { break; } } } for (int i : arr) { System.out.println(i); } } private static void swap(int[] arr, int indexA, int indexB) { int temp = arr[indexA]; arr[indexA] = arr[indexB]; arr[indexB] = temp; } 平均时间复杂度:O(N^2) 最差时间复杂度:O(N^2) 空间复杂度:O(1) 排序方式:In-place 稳定性:稳定