排序算法 - 2.希尔排序(Shell's Sort)

希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”（Diminishing Increment Sort），是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因 D.L.Shell 于 1959 年提出而得名。

 **希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至 1 时，整个文件恰被分成一组，算法便终止。**

（注：为方便记忆算法，我习惯将其记作“三层for循环+if” ------ for（for（for（if））））

2.步骤

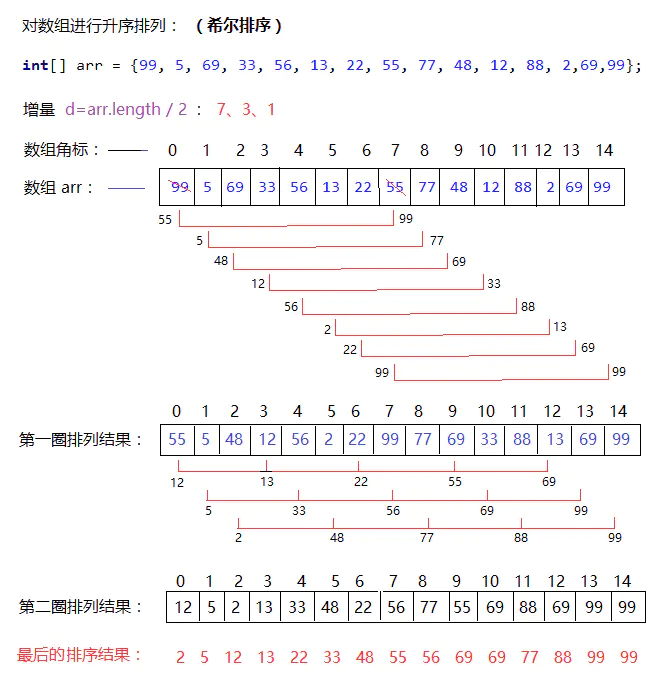
希尔排序的基本步骤，在此我们选择增量gap=length/2，缩小增量继续以gap = gap/2的方式，这种增量选择我们可以用一个序列来表示，{n/2,(n/2)/2...1}，称为增量序列。希尔排序的增量序列的选择与证明是个数学难题，我们选择的这个增量序列是比较常用的，也是希尔建议的增量，称为希尔增量，但其实这个增量序列不是最优的。此处我们做示例使用希尔增量。

    public static void main(String[] args) {
        int[] arr = {99, 5, 69, 33, 56, 13, 22, 55, 77, 48, 12, 88, 2,69,99};
        System.out.println("排序之前数组：");
        printArray(arr);

        //希尔排序
        insertionSort(arr);

        System.out.println("希尔排序后数组：");
        System.out.println(Arrays.toString(arr));

    }
    private static int[]  insertionSort(int[] arr){
        if(arr == null || arr.length <= 1){
            return arr;
        }
        //希尔排序  升序
         // arr.length==15
        for (int d = arr.length / 2;d>0;d /= 2){ //d：增量  7   3   1
            System.out.println("增量取值:" + d);
            for (int i = d; i < arr.length; i++){
                //i:代表即将插入的元素角标，作为每一组比较数据的最后一个元素角标
                //j:代表与i同一组的数组元素角标
                for (int j = i-d; j>=0; j-=d){ //在此处-d 为了避免下面数组角标越界
//                    System.out.println("i:" + i + "  j:" + j +"   j+d="+(j+d));
                    if (arr[j] > arr[j + d]) {// j+d 代表即将插入的元素所在的角标
                        //符合条件，插入元素（交换位置）
                        swap(arr,j,j+d);
                    }
                }
            }
            /*测试:此段代码只为查看希尔排序的每次增量变化过程，正常写程序时不要添加星号注释的这部分代码*/
            for (int m = 0; m < arr.length; m++) {
                System.out.print(arr[m] + " ");
            }
            System.out.println("");
            /**/

        }
        return arr;
    }

    /*
   发现无论什么排序。都需要对满足条件的元素进行位置置换。
   所以可以把这部分相同的代码提取出来，单独封装成一个函数。
   */
    public static void swap(int[] arr,int a,int b)
    {
        int temp = arr[a];
        arr[a] = arr[b];
        arr[b] = temp;
    }
    /*
     * 最近才知道打印数组不用自己写方法这么麻烦，java API中就有 Arrays.toString(arr);
     * 越简单的越容易忽略，这是最后一次自己写这个方法，以后就用自带的方法
     */
    public static void printArray(int[] arr)
    {
        System.out.print("[");
        for(int x=0; x<arr.length; x++)
        {
            if(x!=arr.length-1){
                System.out.print(arr[x]+", ");
            }else{
                System.out.println(arr[x]+"]");
            }

        }
    }

希尔排序的执行时间依赖于增量序列。

希尔排序耗时的操作有：比较 + 后移赋值。

时间复杂度情况如下：（n指待排序序列长度）

1) 最好情况：序列是正序排列，在这种情况下，需要进行的比较操作需（n-1）次。后移赋值操作为0次。即O(n)

2) 最坏情况：O(nlog2n)。

3) 渐进时间复杂度（平均时间复杂度）：O(nlog2n)